How To Calculate Rifling Twist Rates For Stabilizing Bullets

Art Merrill, Field Editor

posted on November 5, 2019

News

Support NRA Shooting Sports USA DONATE

Above: Even excellent match-grade 5.56 mm/.223 Rem. bullets won’t shoot accurately without applying the proper twist. The 55-grain Hornady (l.) should get a 1:12-inch; the 80-grain Sierra (r.), a 1:8- or 1:7-inch.

How heavy or light a bullet will your rifle accurately shoot? In 1879, British mathematician Alfred Greenhill developed a simple formula for determining rifling twist rates for stabilizing bullets. Though overtaken somewhat by updated math and software programs, the Greenhill Formula remains an easy pencil and paper tool today.

Sir Alfred George Greenhill developed his rifling twist rate formula in 1879, and it still works today.

Old concept

The rifling of barrels goes back to the late 1400s, with an earliest known date of 1498 and originating at Augsburg, Germany. It’s possible that rifling appeared independently at different places at relatively the same time but, like the inventions of gunpowder and the earliest firearm ignition systems, if we can attribute the invention of rifling to a single individual, that name is lost to the erosion of time.

One need not study calculus to understand that a spinning bullet is more stable, and therefore more accurate than one that does not spin. The concept is almost intuitive to the curious mind; children learn this early when they play with gyroscopes or tops, or even spinning a coin to stand it on edge. What isn’t known, however, is just why someone thought to apply the concept to round lead ball projectiles. One explanation is that an experimenter cut straight grooves in a rifle barrel to allow easier reloading of a fouled muzzleloading bore, the idea being the fouling has a place to deposit below the bore surface—in the grooves. Extrapolating the idea, spiraling the grooves allows longer (more) grooving for more fouling to deposit within them; discovering the stabilizing effect of the grooves (since called rifling) on the round ball may have been completely unintended.

How much twist?

Of course, the more turns the rifling makes in the bore—the twist rate—the faster the projectile will spin. What remained to be discovered is just how fast a round ball needed to spin to be stabilized for greater accuracy. That is, what twist rate for rifling?

Twist rate is expressed as a ratio of how many complete 360-degree turns the rifling makes per inch of barrel, such as 1:10-inch meaning one complete twist per 10 inches. Note that barrel length has no bearing on the twist rate; a rate of 1:10 remains 1:10 whether a barrel is three inches or three feet long. Experimenters found that stabilizing larger diameter balls required less spin than smaller balls; for example, a .32 caliber round ball is adequately stabilized with a 1:48-inch twist, while for a .50 caliber ball a 1:66-inch does nicely. Finding these rates for round balls was a trial-and-error process, and barrel makers generally settled upon a standard twist rate for each caliber.

However, shooting elongated bullets, whether short, blunt lead muzzleloading conicals or modern secant ogive match grade stuff is a completely different matter. Shooters discovered a rule reversal in that the longer (heavier) the elongated bullet, the faster it needs to spin for stabilization. We see this in High Power and the AR-15 today. While a 1:12-inch twist stabilized early 52- and 55-grain 5.56 mm bullets for the M-16, stepping up to the 62-grain bullet required a 1:10-inch twist.

Heavier/longer 69-, 75- and 77-grain 5.56 mm/.223 Rem. bullets may also perform well with a 1:10-inch twist, but a faster 1:8-inch twist might be better, depending upon the specific bullet. Bullets of 80 and 90 grains now being used at the High Power 600-yard line require twists of 1:8- or 1:7-inch, and the appearance of 100-grain bullets has brought out barrels of 1:6.5-inch twist.

A too-slow twist rate will fail to stabilize the bullet, which will yaw and eventually tumble. We see this on the competition range as bullets “keyholing” the target as they strike the target sideways. So, why not just settle on a 1:6.5-inch twist for all 5.56 mm/.223 Rem. barrels? Because twist rates can also be too high, centrifugal force essentially spinning a bullet’s jacket away from the core and causing a loss of accuracy due to bullet deformation, or the bullet disintegrating completely in flight. There is also argument about “overstabilization,” which may occur because a bullet rotating at too-high speed keeps its nose pointed in the direction of the bore, rather than tangent to its arcing flight path, also reducing accuracy.

Easy math

The advent of elongated bullets called for some kind of mathematical rule of thumb for determining twist rates, as utilizing the trial-and-error solution for every bullet weight for every caliber would be onerous indeed. Enter Professor Sir Alfred George Greenhill of the British Royal Military Academy, who devised a formula for determining twist rate which, simplified here, multiplies the square of the bullet diameter by 150 and then divides the result by the length of the bullet, and looks like this: (C x D²) ÷ L = T.

C is a constant, 150; D² is bullet diameter multiplied by itself, L is bullet length and T is the result, twist rate. Using it is simple; let’s stick with our 5.56 mm/.223 Rem. example. The bullet diameter is .244" and length of a 55 grainer is .740". Following Greenhill:

Step 1—Finding D²: .244 x .244 = .05953
Step 2—Finding C x D²: 150 x .05953 = 8.9295
Step 3—Divide result by bullet length: 8.9295 ÷ .740 = 12.06

So, 1:12.06-inch, rounded to 1:12-inch, is our standard twist rate for the .223 Rem. 55-grain bullet.

Doing the same for an 80-grain bullet 1.075" long:

Step 1—Finding D²: .244 x .244 = .05953
Step 2—Finding C x D²: 150 x .05953 = 8.9295
Step 3—Divide result by bullet length: 8.9295 ÷ 1.075 = 8.306

Rounded, 1:8-inch twist is Greenhill’s indicated twist rate for 80-grain bullets. As shooters have discovered, the reality is that a 1:8-inch twist can be marginal for a .223 Rem. 80-grain bullet, working better with some makes than others, and that a 1:7-inch twist may work better. What’s up with that?

Plug and play math

John Maynard converted Greenhill’s formula into a chart in 1962.

The shortcoming of Greenhill’s formula is that the professor developed it for elliptical (football-shaped) subsonic lead projectiles (he was more into rifled cannons). Though it applies surprisingly well for rifle bullets with muzzle velocities up to about 2,800 fps (for higher velocities, we can substitute 180 for 150 in the constant C, which results in slower twist rates), it isn’t perfect. Others have offered their own (pardon the pun) twists on Greenhill. The Miller twist rule, formulated by Don Miller and published in 2005, refines Greenhill a bit by including bullet weight. The tweak takes into account the lighter-for-length jacketed, hollow point and homogeneous metal bullets invented since Greenhill developed his formula.

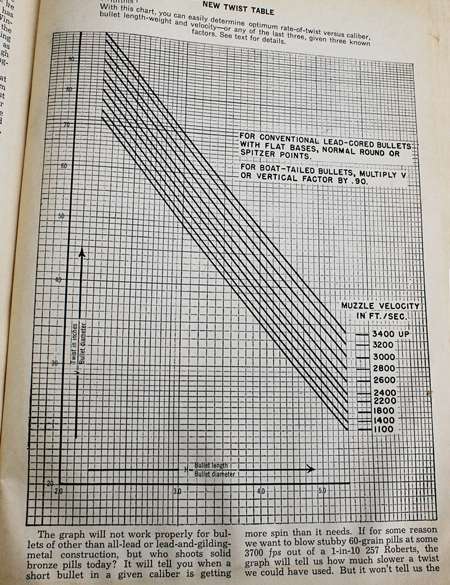
Though Greenhill and Miller may appear complex to those who believe numbers and letters are a devil’s mix, they are both actually simple “plug n play” tools where you plug in your variables, such as bullet length, into the correct place and then let a simple hand calculator do the math. If that’s still too much math, a twist table by John Maynard published in the 1963 Gun Handbook provides an instant, follow-the-lines visual graph. “The graph will not work properly for bullets of other than all-lead or lead-and-gilding metal construction,” Maynard accedes, “but who shoots solid bronze pills today?”

WinGyro by gunsmith John Knight is a free software program that performs twist rate calculations. There’s also the McCoy “McGyro” algorithm drag/twist calculator. You might try the Bowman-Howell software calculator, which requires simple inputs of bullet length, diameter, muzzle velocity and a provided specific gravity density value assigned to copper, brass, lead or steel (the longer version of Greenhill’s formula included specific gravities, as well). It improves upon Greenhill’s formula, which lacks a velocity term, but apparently is not as accurate as Miller across a broader range of muzzle velocities and bullet shapes.

As a final matter of curiosity, how fast do bullets spin, anyway? That depends upon twist rate and muzzle velocity. A 5.56 mm/.223 Rem. bullet fired at 3,000 fps from our National Match AR-15 with a 1:7-inch twist exceeds 300,000 rpm. While we don’t need to know that, we do need to know what bullets our rifles will stabilize, and if we don’t have computers or calculators handy, we can figure it out reasonably well ourselves with pencil and paper—and Greenhill’s formula.

Read more articles by Art Merrill: